ใน คณิตศาสตร์และวิทยาการคอมพิวเตอร์ พีชคณิตแบบบูล, พีชคณิตบูลีน หรือ แลตทิซแบบบูล คือ โครงสร้างเชิงพีชคณิตที่รวบรวมแก่นความหมายของการดำเนินการทางตรรกศาสตร์ นั่นคือ AND, OR, และNOT รวมไปถึงการดำเนินการทางเซต นั่นคืออินเตอร์เซกชัน, ยูเนียน และส่วนเติมเต็ม
ชื่อของพีชคณิตนั้น ตั้งตามจอร์จ บูล นักคณิตศาสตร์ชาวอังกฤษ ที่มหาวิทยาลัย College Cork ผู้ที่นิยามพีชคณิตดังกล่าวขึ้นมาเพื่อเป็นส่วนหนึ่งของระบบทางตรรกศาสตร์ในกลางคริสต์ศตวรรษที่ 19 พีชคณิตแบบบูลนำเทคนิคทางพีชคณิตมาใช้กับนิพจน์ในตรรกศาสตร์เชิงประพจน์ ในปัจจุบันพีชคณิตแบบบูลได้ถูกนำไปประยุกต์อย่างแพร่หลายในการออกแบบทางอิเล็กทรอนิกส์ ผู้ที่นำไปใช้คนแรกคือคลาวด์ อี. แชนนอนในคริสต์ศตวรรษที่ 20
ตัวดำเนินการในพีชคณิตแบบบูลสามารถเขียนได้หลายแบบ โดยมากแล้วเราจะเขียนเป็น AND, OR, และ NOT ในการออกแบบวงจร NAND (NOT AND), NOR (NOT OR) และ XOR (eXclusive OR) ก็มีการใช้ทั่วไป นักคณิตศาสตร์ มักใช้ + สำหรับ OR และ · แทน AND (เนื่องจากตัวดำเนินการเหล่านี้มีลักษณะคล้ายคลึงกับการบวก และการคูณ ในโครงสร้างเชิงพีชคณิตอื่นๆ) และเขียน NOT ด้วยเส้นขีดเหนือนิพจน์ที่ถูกนิเสธ

นิยาม
พีชคณิตแบบบูล คือ เซต A ที่ประกอบด้วยการดำเนินการทวิภาค คือ (AND) กับ (OR), การดำเนินการเอกภาค คือ / ~ (NOT) และสมาชิกคือ 0 (FALSE) กับ 1 (TRUE) ซึ่งสำหรับสมาชิก a, b และ c ของเซต A จะมีคุณสมบัติเป็นไปตามสัจพจน์เหล่านี้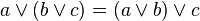

		การเปลี่ยนหมู่
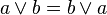		การสลับที่
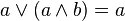		absorption
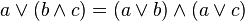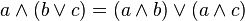		การแจกแจง
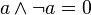		ส่วนเติมเต็ม

สำหรับสมาชิก a และ b ใน A มันจะมีเอกลักษณ์ดังต่อไปนี้

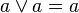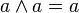		นิจพล (idempotency)
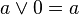		มีขอบเขต (boundedness)
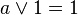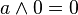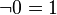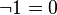		0 และ 1 เป็นส่วนเติมเต็มกัน
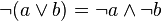		กฎเดอมอร์แกน (de Morgan's laws)
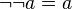		อวัตนาการ (involution)